1.1 场论基础

• 场的概念:指带有某种物理量的空间
  • 数学语言描述:如果空间或部分空间中每一点对应于某一量的值，则这样的空间称为场
• 方向导数:$\frac{\partial u}{\partial l}=\lim _{P \rightarrow P} \frac{u\left(P_{1}\right)-u(P)}{\overline{P_{1} P}}$存在,为场u(P)在P点沿$\vec{l}$方向的方向导数,记为$\frac{\partial u}{\partial l}$
• 梯度$\nabla U$:
  • 方向为使$u(P)$在P点方向导数最大的方向(与等值面法线平行)
  • 模为方向导数最大方向上的方向导数
  • 哈密顿算符’del’:$\nabla=\frac{\partial}{\partial x} \vec{i}+\frac{\partial}{\partial y} \vec{j}+\frac{\partial}{\partial z} \vec{k}$
• 散度$\nabla \cdot \vec{A}$:
  • 流量:对任意矢量场$\vec{A}(P)$, 称式$\oint_{s} \vec{A}\bullet d s=\oint_{s}\vec{A} \bullet \vec{N} ds$为通过封闭曲面$S$的流量
    • =0 S内无源也无沟
    • >0 S内有源
    • <0 S内有沟
  • $\frac{\oint_s \vec{A} \bullet ds}{V}$单位体积内的源发出的液量大小,V中源的平均强度
  • 散度:$\nabla \cdot \vec{A}=lim_{D(V) \rightarrow 0} \frac{\oint_s \vec{A} \bullet ds}{V}$,P点处源的平均强度,称矢量$\vec{A}$在P点的散度
  • 物理意义:表示矢量场中某点通量源的密度
    • 若散度为0,表示无散场
    • 若散度为$\rho(源密度)$,表示有散场
  • 计算:
    • $\operatorname{div} \vec{A}(\vec{r})=\frac{\partial A_{x}}{\partial x}+\frac{\partial A_{y}}{\partial y}+\frac{\partial A_{z}}{\partial z}$
    • $\nabla \cdot \vec{A}=\frac{1}{r} \frac{\partial\left(r A_{r}\right)}{\partial r}+\frac{1}{r} \frac{\partial A_{\varphi}}{\partial \varphi}+\frac{\partial A_{z}}{\partial z}$
    • $\nabla \cdot \vec{A}=\frac{1}{r^{2}} \frac{\partial}{\partial r}\left(r^{2} A_{r}\right)+\frac{1}{r \sin \theta} \frac{\partial}{\partial \theta}\left(\sin \theta A_{\theta}\right)+\frac{1}{r \sin \theta} \frac{\partial A_{\varphi}}{\partial \varphi}$
  • 性质:
    • $\nabla \cdot(\alpha \vec{A}+\beta \vec{B})=\alpha \nabla \cdot \vec{A}+\beta \nabla \cdot \vec{B}$
    • $\nabla \cdot(u \vec{A})=u \nabla \cdot \vec{A}+\vec{A} \cdot \nabla u \quad(u$
  • 散度定理(矢量场中的高斯定理):$\int_{V} \nabla \cdot \vec{A} d V=\oint_{s} \vec{A} \cdot d \vec{S}$
    • 物理意义:矢量场$\vec{A}$的散度在体积V内的体积分等于矢量场穿过包围该体积的闭合边界面S的面积分
    • 体积V内通量为:$\Psi=\int_{V} \nabla \cdot \vec{A} d V$
• 旋度$\nabla \times \vec{A}$:
  • 环流:
    • 矢量场$\vec{A}(P)$中,沿封闭曲线$\Gamma$的线积分$\oint_{\Gamma} \vec{A} \cdot d \vec{l}$
    • 物理意义:若矢量场环流不为0,则说明场中有在矢量场的漩涡源,不能显示源的分布情况
  • 环流密度:$W_{n} (P)=\lim_{D(s) \rightarrow 0} \frac{\oint_{\Gamma} \vec{A} \cdot d \vec{l}}{S}$
  • 环流面密度:空间某点M处沿单位面元边界闭合曲线的环流称为矢量场$\vec{F(\vec{r})}$在M点处沿$\vec{e_n}$方向的环流面密度
    • $\operatorname{rot} \vec{F}=\vec{n} \lim _{\Delta S \rightarrow 0} \frac{\oint_{c} \vec{F} \cdot d \vec{l}}{\Delta S}$
  • 旋度:矢量场在M点的旋度为该点处的最大环流面密度，其方向为环流面密度取得最大值的面元法线方向
    • $\operatorname{rot} \vec{F}=\left.\vec{n} \lim _{\Delta S \rightarrow 0} \frac{\oint_{c} \vec{F} \cdot d \vec{l}}{\Delta S}\right|_{\max }$
  • 物理意义:矢量场的旋度表征了矢量场在空间某点处的漩涡源密度
  • 计算:$\operatorname{rot} \vec{A}=\nabla \times \vec{A}=\left|\begin{array}{ccc}\vec{i} & \vec{j} & \vec{k} \\ \frac{\partial}{\partial x} & \frac{\partial}{\partial y} & \frac{\partial}{\partial z} \\ A_{x} & A_{y} & A_{z}\end{array}\right|$
  • 斯托克斯定理:矢量场的旋度在曲面S上的面积分等于该矢量场沿限定该曲面的闭合路径C上的线积分
    • $\oint_{C} \vec{F} \cdot \mathrm{d} \vec{l}=\int_{S} \nabla \times \vec{F} \cdot \mathrm{d} \vec{S}$
• 势函数,势量场(保守场),矢势
  • 对矢量场$\vec{A_p}$存在单值函数$u(P)$,使$\vec{A} = \nabla u$,称$\vec{A}(p)$为势量场,$u(p)$为势量场$\vec{A}_(p)$的势函数.
  • 保守场:
    • 无旋$\nabla \times \nabla u \equiv 0$
    • 回路积分为0
    • 例如:重力场,静电场
  • 对无旋场$\vec{A}$势函数$u$为标量,$u$为势量场的标势
  • 矢势:
    • 对无源场存在矢势$\vec{A}$使$\vec{B} \equiv \nabla \times \vec{A}$(无源势必存在矢势$\nabla \bullet(\nabla \times \vec{A})$
  • 有散无旋场(有势场,保守场):标量位函数$u$的梯度表征矢量场$\nabla \times(\nabla \bullet \vec{A}) \equiv 0$
  • 无散有旋场(管形场):引入矢量位函数$A$的旋度,表示无散场,恒磁场$\nabla \bullet B \equiv 0 \rightarrow \vec{B} = \nabla \times A$

1.2 静电场,静磁场基本定律

1.2.1 静电场

• 库伦定理:$\mathbf{F}_{12}=\frac{q_{1} q_{2}}{4 \pi \varepsilon_{0} R_{12}^{2}} \hat{\mathbf{e}}_{R}=\frac{q_{1} q_{2}}{4 \pi \varepsilon_{0} R_{12}^{3}} \mathbf{R}_{12}$
  • $\varepsilon_{0} \approx(36 \pi)^{-1} \times 10^{-9} \mathrm{~F} / \mathrm{m}=8.8542 \times 10^{-12} \mathrm{~F} / \mathrm{m}$
  • 电场强度:$\mathbf{E}=\lim _{q_{0} \rightarrow 0} \frac{\mathbf{F}}{q_{0}}=\frac{q}{4 \pi \varepsilon_{0} R^3} \vec{R}$
• 高斯定理:
  • $\oint_{S} \mathbf{E}(\mathbf{r}) \cdot \mathrm{d} \mathbf{S}=\frac{1}{\varepsilon_{0}} \sum_{i} q_{i}=\frac{Q}{\varepsilon_{0}}$
  • $\nabla \cdot \mathbf{E}(\mathbf{r})=\frac{\rho(\mathbf{r})}{\varepsilon_{0}}$
  • 物理意义:
    • 静电场穿过闭合面𝐒的通量只与闭合面内所围电荷量有关
    • 静电场是有源场，静电荷是其散度源
• 静电场环路定律
  • $\oint_{C} \mathbf{E} \cdot \mathrm{d} \mathbf{l}=0$
  • $\nabla \times \mathbf{E}(\mathbf{r})=0$
  • 物理意义:静电场为无旋场(保守场)(电场力不做功——闭合环路)
  • 静电场为有源无旋场,恒有$\nabla \times \mathbf{E}=0 \Rightarrow \nabla \times(\nabla \varphi) \equiv 0 \quad \Rightarrow \quad \mathbf{E}=-\nabla \varphi$,静电场可由势函数的梯度表示
    • 均匀介质中,$\left.\begin{array}{l}\nabla \cdot \mathbf{E}=\frac{\rho}{\varepsilon} \\ \mathbf{E}=\nabla(-u)\end{array}\right\}$
      • 故电势的标量泊松方程$\nabla^{2} u=-\frac{\rho}{\varepsilon}$
    • 无源区域$\rho =0$,拉普拉斯方程$\nabla^{2} u=0$

1.2.2 静磁场

• 体电流密度:$\mathbf{J}=\lim _{\Delta t \rightarrow 0} \frac{\Delta i}{\Delta S} \hat{\mathbf{e}}_{n}=\frac{\mathrm{d} i}{\mathrm{~d} S} \hat{\mathbf{e}}_{n}=\rho \mathbf{v}$,单位$C/(s*cm^2)$或$A/cm^2$
• 电流强度:单位时间内通过垂直穿过任意截面积 𝐒 的电量
  • $I=\int_{S} \mathbf{J} \cdot \mathrm{d} \mathbf{S}=\int_{S} \mathbf{J} \cdot \widehat{\mathbf{n}} \mathrm{d} S$
• 电流连续性方程
  • $\oint_{S} \mathbf{J} \cdot \mathrm{d} \mathbf{S}=-\frac{\mathrm{d} q}{\mathrm{~d} t}=\int_{V}-\frac{\partial \rho}{\partial t} \mathrm{~d} V$
  • $\nabla \cdot \mathbf{J}+\frac{\partial \rho}{\partial t}=0$
  • 单位时间内从体积𝑉中减少的电荷量等于流出该体积总电流
  • 导电介质中的欧姆定律(微分形式):$\mathbf{J}_{c}=\sigma \mathbf{E}$
• 安培力公式:$\mathbf{F}_{12}=\frac{\mu_{0}}{4 \pi} \oint_{C_{2}} I_{2} \mathrm{~d} \vec{\mathbf{l}_{2}} \times \oint_{C_{1}} \frac{I_{1} \vec{\mathrm{dl}_{1}} \times \vec{\mathbf{e}_{R}}}{R_{12}^{2}}$
• 毕奥－萨伐尔定律:$\vec{B}(\mathbf{r})=\frac{\mu_{0}}{4 \pi} \oint_{C} \frac{I \mathrm{~d} \vec{\mathbf{l}^{\prime}} \times \vec{\mathbf{R}}}{R^{3}}$,单位$T,W/m^2$
• 磁通连续性原理:
  • $\oint_{\mathbf{S}} \vec{\mathbf{B}} \cdot \mathrm{d} \vec{S}=0$
  • $\nabla \cdot \vec{B}=0$
  • 恒定磁场中，磁感应强度矢量穿过任意闭合面的磁通量为零
  • 恒定磁场无散度源,磁力线是闭合连续的
• 安培环路定律:
  • $\oint_{C} \vec{B}(\mathbf{r}) \cdot \mathrm{d} \vec{l}=\mu_{0} \sum_{k} I_{k}=\mu_{0} I$
  • $\nabla \times \vec{B}(\mathbf{r})=\vec{\mu_{0}}(\mathbf{r}) \mathbf{J}$
  • 在恒定磁场中，磁感应强度在任意闭合回路𝐿上的环流等于穿过回路𝐿所围面积𝑆内电流的代数和与$\mu_0$的乘积
  • 静磁场有旋场，涡流源是恒定电流

1.3 时变电磁场

• 电磁感应定律:
  • $\oint_{C} \mathbf{E} \cdot \mathrm{d} \mathbf{l}=-\int_{S} \frac{\partial \mathbf{B}}{\partial t} \cdot \mathrm{d} \mathbf{S}$
  • $\nabla \times \mathbf{E}=-\frac{\partial \mathbf{B}}{\partial t}$
  • 当穿过导体回路所围面积的磁通量发生改变时,回路中将产生感应电动势， 其大小等于回路磁通量的时间变化率
  • 物理意义:随时间变化的磁场将产生电场
  • 涡旋电场:时变电磁场的主要区别之一:与静电场不同，当磁场为时变的情况时，电场的旋度不再为零,而是涡旋电场
• 全电流定律:
  • $\nabla \times \mathbf{B}=\mu_{0} \mathbf{J}+\mu_{0} \frac{\partial \mathbf{D}}{\partial t}$
  • 物理意义:磁场的激发源不仅仅是传导电流，还可以是变化的电场
  • 位移电流:在时变场空间中,存在着因变化的电场而形成的位移电流,位移电流与自由电流共同形成全电流
    • 理想介质中,无传导电流,但可能有位移电流
    • 理想导体中,无位移电流,但可能有传导电流
    • 导电介质中,既可能有传导电流,又可能有位移电流

1.4 真空中的麦克斯韦方程组

1.5 介质中的麦克斯韦方程组

• 极化
  • 电介质:指导线性能较差的为u之
  • 电偶极子:由两个相距很近且带等量异号电量的点电荷所组成的电荷系统,用电偶极矩描述,$\vec{p} = q \vec{d}$
    • 无极分子:电偶极矩为0,正负电荷中心重合((外加电场后,无极分子位移极化)
    • 有极分子:电偶极矩不为0,正负电荷中心不重合(外加电场后,有极分子取向极化)
  • 极化过程:外加电场使电介质极化,产生极化电荷;极化电荷又形成极化电场,两者相互制约并达到平衡状态
  • 极化强度矢量:极化强度矢量是描述介质极化程度的物理量$\mathbf{P}=\frac{\left(\sum \mathbf{p}_{i}\right)_{\Delta V}}{\Delta V}=n \mathbf{p}$
    • 物理意义:单位体积内分子电偶极矩的矢量和
  • 极化电荷体密度:
    • 极化电荷数:$q_{\mathrm{P}}=-\int_{V} \rho_{\mathrm{P}} \mathrm{d} V=\oint_{S} \mathbf{P} \cdot \mathrm{d} \mathbf{S}=\int_{V} \nabla \cdot \mathbf{P} \mathrm{d} V$
      • 极化电荷体密度:$\rho_{\mathrm{P}}=-\nabla \cdot \mathbf{P}$
      • 极化电荷面密度:$\rho_{\mathrm{sp}}=\mathbf{P} \cdot \mathbf{e}_{\mathrm{n}}$
    • 极化电流(密度):$\mathbf{J}_{\mathrm{P}}=\frac{\partial \mathbf{P}}{\partial t}$
• 电介质中的高斯定理:
  • 电位移矢量:$D=\varepsilon_0E+P$
  • $\nabla \cdot D = \rho_f$
  • $\int_{s} D dS=Q_f$
  • 本构关系:$D=\varepsilon_0(1+\varkappa_e)E=\varepsilon_0\varepsilon_r E = \varepsilon E$
    • $\varepsilon_r =1+\varkappa_e$相对介电常数
    • $\varepsilon = \varepsilon_0\varepsilon_r$绝对介电常数
• 磁化
  • 分子电流:电子绕原子核运动形成"分子电流"
  • 磁偶极矩:分子电流产生磁偶极矩$\vec{m}=i\vec{a}$
  • 磁介质的磁化
    • 外加磁场时:大量磁偶极矩的取向与外加磁场趋于一致,宏观上表现出磁特性,这一过程称为磁化
  • 磁化强度矢量:单位体积内的磁偶极矩的磁化强度矢量
    • $\mathbf{M}=\frac{\left(\sum \mathbf{m}_{i}\right)_{\Delta V}}{\Delta V}=n \mathbf{m}$
  • 磁化电流:磁介质被磁化后,在其内部和表面将出现宏观磁化电流
  • 磁化电流密度:$\mathbf{J}_{\mathrm{M}}=\nabla \times \mathbf{M}$
  • 磁介质中安培环路定律:
    • 磁场强度矢量$\vec{H}=\frac{\vec{B}}{\mu_0} - \vec{M}$
    • $\nabla \times \mathbf{H}=\mathbf{J}_{\mathrm{f}}+\frac{\partial \mathbf{D}}{\partial t}$
    • $\int_{C} \mathbf{H} \cdot \mathrm{d} \mathbf{l}=\int_{S}\left(\mathbf{J}_{\mathrm{f}}+\frac{\partial \mathbf{D}}{\partial t}\right) \cdot \mathrm{d} \mathbf{S}$
    • 磁介质本构关系:
      • $\mathbf{B}=\mu_{0}\left(1+\chi_{\mathrm{m}}\right) \mathbf{H}=\mu_{0} \mu_{\mathrm{r}} \mathbf{H}=\mu \mathbf{H}$

• 电磁场的源:电流和电荷;时变的电场和时变的磁场
• 无源空间中的两个旋度方程为:
  • $\nabla \times \mathbf{H}= \frac{\partial \mathbf{D}}{\partial t}$
  • $\nabla \times \mathbf{E}=-\frac{\partial \mathbf{B}}{\partial t}$
  • 在离开辐射源(如天线)的无源空间中,电荷密度和电流密度矢量为零,电场和磁场相互激发,从而在空间形成电磁振荡并传播,这就是电磁波时变磁场
  • 时变电磁场中，电场和磁场相互关联，构成一个整体。静场只是时变场的一种特殊情况
• 麦克斯韦方程组的物理含义:
  • 时变电场的激发源除电荷以外,还有变化的磁场
  • 时变磁场的激发源除传导电流以外,还有变化的电场
  • 电场和磁场可互为激发源
• 静电场,静磁场
  • 在静态情况下𝐄和𝐃与静磁场中的𝐁和𝐇是相互独立的矢量对,它们互不相关
• 时变电磁场
  • 变化的电场可以激励出时变的磁场,而时变的磁场又可激励出时变电场

1.6 电磁场的边界条件

• 电场强度E的边界条件:
  • $\oint_{C} \mathbf{E} \cdot \mathrm{d} \mathbf{l}=-\int_{S} \frac{\partial \mathbf{B}}{\partial t} \cdot \mathrm{d} \mathbf{S}$
  • $\Delta h\rightarrow 0,\Rightarrow \vec{n} \times (\vec{E_2}-\vec{E_1})=0$
  • $(\vec{E_{2t}}-\vec{E_{1t}})=0$
  • 在分界面上电场强度矢量的切向分量连续
• 磁场强度H的边界条件:
  • $\oint_{C} \mathbf{H} \cdot \mathrm{d} \mathbf{l}=\int_{S} (\mathbf{J}+\frac{\partial \mathbf{D}}{\partial t}) \cdot \mathrm{d} \mathbf{S}$
  • $\Delta h\rightarrow 0,\Rightarrow \vec{n} \times (\vec{H_2}-\vec{H_1})=\vec{J_s}$
  • $(\vec{H_{2t}}-\vec{H_{1t}})=\vec{J_s}$
  • 在分界面上磁场矢量的切向分量与界面处自由面电流相关
  • 当界面处自由面电流为0时,磁场强度矢量切向分量在界面处连续
• 电位移矢量D的边界条件:
  • $\oint_{S} \mathbf{D} \cdot \mathrm{d} \mathbf{S} = Q$
  • $\Delta h\rightarrow 0,\Rightarrow \vec{n} \cdot (\vec{D_2}-\vec{D_1})=\rho_s$
  • $(\vec{D_{2n}}-\vec{D_{1n}})=\rho_s$
  • 在介质界面上电位移矢量的法向分量与界面处自由面电荷相关
  • 当界面处自由面电荷为0时,电位移矢量法向分量在界面处连续
• 磁感应矢量B的边界条件:
  • $\oint_{S} \mathbf{B} \cdot \mathrm{d} \mathbf{S} = 0$
  • $\Delta h\rightarrow 0,\Rightarrow \vec{n} \cdot (\vec{B_2}-\vec{B_1})=0$
  • $(\vec{B_{2n}}-\vec{B_{1n}})=0$
  • 在介质界面上磁感应强度矢量法向分量连续

1.7 无源波动方程

• 无源波动方程的一般形式
  • 推导过程:
    • 矢量恒等式:$\nabla \times \nabla \times \mathbf{A}=\nabla(\nabla \cdot \mathbf{A})-\nabla^{2} \mathbf{A}$
    • 无源均匀简单介质,$J=0,\rho=0,D=\varepsilon E,B=\mu H$
    • 由$\nabla \times \mathbf{E}=-\frac{\partial \mathbf{B}}{\partial t}$,取散度可得,$\nabla \times \nabla \times \mathbf{E}=\nabla \times (-\mu \frac{\partial \mathbf{H}}{\partial t})$,利用恒等式,且$\nabla\cdot \mathbf{D}=0$,可得$\nabla^{2} \mathbf{E}-\mu \varepsilon \frac{\partial^{2} \mathbf{E}}{\partial t^{2}}=0$
  • 波动方程:
    • $\nabla^{2} \mathbf{E}-\mu \varepsilon \frac{\partial^{2} \mathbf{E}}{\partial t^{2}}=0$,$\nabla^{2} \mathbf{H}-\mu \varepsilon \frac{\partial^{2} \mathbf{H}}{\partial t^{2}}=0$
    • 令$v=\frac{1}{\sqrt{\varepsilon \mu}}$为介质中电磁波传播速度,$n=\sqrt{\varepsilon_r \mu_r}$
    • $\nabla^{2} \mathbf{E}-\frac{1}{v^2} \frac{\partial^{2} \mathbf{E}}{\partial t^{2}}=0$,$\nabla^{2} \mathbf{H}-\frac{1}{v^2} \frac{\partial^{2} \mathbf{H}}{\partial t^{2}}=0$
    • 结论:
      • 电磁场具有波动性，以波的形式向外传播
      • 电磁波的传播速度为𝑣,𝑣取决于传播介质
• 时谐电磁场,定态波动方程
  • 电场表示为复振幅形式$E(r,t)=E(r)e^{iwt}$
  • 代入波动方程可得:$\nabla^{2}E+ w^2 \mu \varepsilon E=0$
  • 波数:$k=w\sqrt{\mu \varepsilon} = \frac{2\pi}{\lambda}$
  • 定态波动方程–亥姆赫兹方程
    • $\nabla^{2}E+ k^2 E=0$
    • $\nabla^{2}H+ k^2 H=0$
• 非均匀介质中波动方程(无源非均匀介质)
  • $J_s=0,\rho_s=0，D(r)=\varepsilon(r)E(r),B(r)=\mu_0H(r)$
  • 故可推导电场波动方程,磁场波动方程

1.9 电磁场的能量

• 带电粒子或系统在电磁场中所受的力:洛伦兹力
  • 电场力:$\vec{F}=q\vec{E}$
  • 磁场力:$\vec{F} = q\vec{v} \times \vec{B}$
• 能量密度:场内单位体积内电磁场的能量
• 能流密度:(坡印廷矢量),表示电磁场传输的功率面密度($W/m^2$)
  • 方向为能量传输方向,数值等于单位时间内垂直流过单位横截面积的能量
  • 坡印廷定理:$-\nabla \cdot \mathbf{S}=\mathbf{f} \cdot \mathbf{v}+\frac{\partial w}{\partial t}$
• 能量密度及能流密度的表达式
  • 电磁场对电荷所作的功:$\vec{f} \cdot \vec{c} = \rho \vec{E} \cdot \vec{v}+ (\vec{J} \times \vec{B}) \cdot \vec{v}$
  • 将$\vec{J} = \rho \cdot \vec{v}$代入可得$\vec{f} \cdot \vec{c} = \vec{E} \cdot \vec{J}$
  • 由坡印廷定理可得:$-\nabla \cdot \mathbf{S} -\frac{\partial w}{\partial t}=\mathbf{f} \cdot \mathbf{v}=E \cdot J$
    • 由$\nabla \times H = J + \frac{\partial D}{\partial t}$,得$J =\nabla \times H - \frac{\partial D}{\partial t}$
    • 而$E \cdot J = E \cdot (\nabla \times H - \frac{\partial D}{\partial t})$
      • $\mathbf{E} \cdot(\nabla \times \mathbf{H})=-\nabla \cdot(\mathbf{E} \times \mathbf{H})+\mathbf{H} \cdot(\nabla \times \mathbf{E})=-\nabla \cdot(\mathbf{E} \times \mathbf{H})-\mathbf{H} \cdot \frac{\partial \mathbf{B}}{\partial t}$
      • $\mathbf{E} \cdot \mathbf{J}=-\nabla \cdot(\mathbf{E} \times \mathbf{H})-\left(\mathbf{E} \cdot \frac{\partial \mathbf{D}}{\partial t}+\mathbf{H} \cdot \frac{\partial \mathbf{B}}{\partial t}\right)$
    • 故由坡印廷定理得:$-\nabla \cdot \mathbf{S} -\frac{\partial w}{\partial t}=E \cdot J = -\nabla \cdot(\mathbf{E} \times \mathbf{H})-\left(\mathbf{E} \cdot \frac{\partial \mathbf{D}}{\partial t}+\mathbf{H} \cdot \frac{\partial \mathbf{B}}{\partial t}\right)$
  • 故$S=E \times H,\frac{\partial w}{\partial t} = \mathbf{E} \cdot \frac{\partial \mathbf{D}}{\partial t}+\mathbf{H} \cdot \frac{\partial \mathbf{B}}{\partial t}$
• 电磁能量的传输
  • 电磁场在传输过程中其能量是以场的形式在传播
  • 传输的总功率为坡印廷矢量在传输空间的截面上的积分:$P=\int_{\Sigma} \mathbf{S} \cdot \mathrm{d} \boldsymbol{\sigma}=\int_{\Sigma}(\mathbf{E} \times \mathbf{H}) \cdot \mathrm{d} \boldsymbol{\sigma}$

2 电磁场在无限大均匀介质中的传播

2.1 无限大均匀介质中的平面波解

• 无源波动方程:$\nabla^{2} \mathbf{E}-\mu \varepsilon \frac{\partial^{2} \mathbf{E}}{\partial t^{2}}=0$
  • 将时谐电磁场$E_i= U_i(r)e^{iwt}$代入,可得亥姆霍兹方程$\nabla^{2} U_i(r)+k^2U_i(r)=0$
  • 可得通解:$U_i(r)=a_i^+e^{-ik \cdot r}+a_i^-e^{ik \cdot r}$
  • 位相共轭波,当正反向传播的波的复振幅互为复数共轭,则称这一对波为位相共轭波

2.2 无限大均匀介质中的球面波解

• $\nabla^{2}=\frac{1}{r^{2}} \frac{\partial}{\partial r}\left(r^{2} \frac{\partial}{\partial r}\right)+\frac{1}{r^{2} \sin \theta} \frac{\partial}{\partial \theta}\left(\sin \theta \frac{\partial}{\partial \theta}\right)+\frac{1}{r^{2} \sin \theta^{2}} \frac{\partial^{2}}{\partial \varphi^{2}}$
• 由亥姆霍兹方程可得:$\frac{1}{r} \frac{\partial^{2}}{\partial r^{2}}[r \mathbf{U}(r)]+k^{2} \mathbf{U}(r)=0$
• 可得解:
  • 发散球面波:$E^+(r,t)=\frac{a^+}{r}e^{i(wt-kr)}$
  • 会聚球面波:$E^-(r,t)=\frac{a^-}{r}e^{i(wt+kr)}$
• 球面单色波:
  • $\vec{E}(r,t) = \frac{a}{r}cos(wt+Kr)$
  • $\vec{E}(r,t) = \frac{a}{r}e^{i(wt+Kr)}$

2.3 无限大均匀介质中柱坐标系下的高斯光束基模解

• $\nabla^{2}=\nabla_{\mathrm{t}}^{2}+\frac{\partial^{2}}{\partial z^{2}}=\frac{\partial^{2}}{\partial r^{2}}+\frac{1}{r} \frac{\partial}{\partial r}+\frac{\partial^{2}}{\partial z^{2}}$
• 由亥姆霍兹方程可得:$\nabla_{\mathrm{t}}^{2} \mathbf{U}(\mathbf{r})+\frac{\partial^{2} \mathbf{U}(\mathbf{r})}{\partial z^{2}}+k^{2} \mathbf{U}(\mathbf{r})=0$
• 能流主要沿Z轴传播的近似平面波:$U(r)=A(r)e^{-ikz}$
• 利用近似平面波方程,振幅沿Z轴缓慢变化,忽略$\frac{\partial^2 \mathbf{A(r)}}{\partial^2 z}$,可得傍轴方程$\nabla_{\mathrm{t}}^{2} A(\mathbf{r})-2 \mathrm{i} k \frac{\partial A(\mathbf{r})}{\partial z}=0$
• 介质均匀$n(r)=n_0$,考察的场矢量在垂直于$z$轴平面上$r$方向上等同,利用$\nabla_{\mathrm{t}}^{2}=\frac{\partial^{2}}{\partial r^{2}}+\frac{1}{r} \frac{\partial}{\partial r}$,可得$\frac{\partial^{2} A(r, z)}{\partial r^{2}}+\frac{1}{r} \frac{\partial A(r, z)}{\partial r}-2 \mathrm{i} k \frac{\partial A(r, z)}{\partial z}=0$
• 解上面的方程:$U(r, z)=A_{0} \frac{w_{0}}{w(z)} \exp \left[-\frac{r^{2}}{w^{2}(z)}\right] \exp \left\{-\mathrm{i}\left[k z+\frac{k r^{2}}{2 R(z)}-\varphi(z)\right]\right\}$
• 激光光学中的基模高斯光束,是波动方程的一个特解,基模解
  • 高斯光束的等相面曲率半径:$R(z)=z\left(1+\frac{z_{0}^{2}}{z^{2}}\right)$
  • 高斯光束的光斑半径:$w(z)=w_{0} \sqrt{1+\frac{z^{2}}{z_{0}^{2}}}$
  • 高斯光束的附加相位因子:$\varphi(z)=\arctan \left(\frac{z}{z_{0}}\right)$
  • 高斯光束的共焦参数:$z_{0}=\frac{\pi w_{0}^{2} n_{0}}{\lambda},\quad z=z_{0}$ 时, $w(z)=\sqrt{2} w_{0}$
• 高斯球面波的性质:
  • 光斑半径$w(z)$:在光束界面内,自光轴轴线到振幅的大小下降至轴线的$1/e$点的距离
    • $\frac{w^2(z)}{w_0^2}-\frac{z^2}{z_0^2} = 1$
  • 等相面:相位相同的点的轨迹
    • 等相面是球面,曲率半径$R(z)$不恒定,是z的函数
    • $R(z)=z\left(1+\frac{z_{0}^{2}}{z^{2}}\right)$
    • 当$z=z_0$,$R(z)$最小,等于$2z_0$;在束腰和无穷远处为平面
    • 等相面的曲率中心随着光束的传输而移动,不是固定的点
  • 总相移:光束在点处相对于原点的相位差
    • $\phi(z)=k\left[z+\frac{r^{2}}{2 R(z)}\right]-\varphi(z)$
  • 瑞利长度$z_0$(共焦参数)
    • $z_{0}=\frac{1}{2} k w_{0}^{2}=\frac{\pi w_{0}^{2}}{\lambda}$
    • 当$|z| = z_0$时,$w(z_0)=\sqrt{2}w_0$
    • 当$|z| \leq z_0$时,对应于准直范围,高斯光束近似平行
    • 瑞利长度越长,高斯光束的准直范围越大
  • 远场发散角$\theta_0$:数值上等于以束宽$w_0$为半径的光束的衍射角
    • $\theta_{0}=\lim_{z \rightarrow \infty} \frac{w(z)}{z}=\frac{\lambda}{\pi w_{0}}$
  • 高斯光束在其传输轴线附近,可近似堪称一种非均匀球面波,曲率中心随传输过程而不断改变,振幅和强度在横截面内始终保持高斯分布特性,等相面始终保持为球面,光强集中在轴线及其附近

2.4 单色平面波的基本性质

• 单色平面波的特点
  • 具有空间周期性和时间周期性
  • 时间和空间上是无限的
  • 若任何时间和空间周期的破坏都意味着单色性遭到破坏.平面波的振幅或位相若受到时间或空间的调制,它的单色性和平面性都受到破坏
  • $E和K的关系$
    • $\nabla \cdot E = 0$将$E=E_0 exp[i(wt-k \cdot r)]$代入可得$\nabla \cdot E = -i k \cdot E = 0 \Rightarrow k \perp E$
    • 单色平面波是横电磁波
  • $E与B的关系$
    • $\nabla \times \mathbf{E}=-\mathrm{i} \omega \mu \mathbf{H}=-\mathrm{i} \omega \mathbf{B}$ & $\hat{\mathbf{e}}_{\mathbf{k}}$
    • $\mathbf{B}=\frac{\mathrm{i}}{\omega} \nabla \times \mathbf{E}=\frac{\mathrm{i}}{\omega} \nabla \times\left\{\mathbf{E}_{0} \exp [\mathrm{i}(\omega t-\mathbf{k} \cdot \mathbf{r})]\right\}=\frac{1}{\omega} \mathbf{k} \times \mathbf{E}=\sqrt{\mu \epsilon} \hat{\mathbf{e}}_{\mathbf{k}} \times \mathbf{E}$
    • 故$B \perp k,B \perp E$
    • E,B,k三者互相垂直
  • 波阻抗
    • 真空中波阻抗:$\eta_{0}=\left|\frac{\mathbf{E}}{\mathbf{H}}\right|=\sqrt{\frac{\mu_{0}}{\varepsilon_{0}}}=\sqrt{\frac{4 \pi \times 10^{-7}}{8.85 \times 10^{-12}}}=120 \pi \approx 377(\Omega)$
    • 波阻抗:$\eta=\left|\frac{\mathbf{E}}{\mathbf{H}}\right|=\sqrt{\frac{\mu}{\varepsilon}}$

2.5 平面波的能量和能流密度

• 平面波的能量密度:
  • 瞬时能量密度:$w=\frac{1}{2}(E \cdot D+ H \cdot B) = \frac{1}{2}(\varepsilon E^2+ \frac{1}{\mu}B^2)=\frac{1}{\mu}B^2$
  • 时间平均能量密度:$< w >= \frac{1}{2} \varepsilon E_0^2$
• 平面波的能流密度(坡印廷矢量):
  • 平面电磁波情况: $B=\sqrt{\mu \varepsilon} e_k \times E$
  • 瞬时能流密度$S = E\times H=\frac{1}{\sqrt{\mu \varepsilon}}we_k=v_\phi w e_k$
  • 平均能流密度:$< S >=\frac{1}{2}\sqrt{\frac{\varepsilon}{\mu}} E_0^2 e_k$
  • 能流密度大小=能量密度×相速度
  • 能流密度方向为波矢量的方向
    • 光学中,通常将时间平均能量密度成为光强

2.6 准单色光波

• 准单色光波的物理意义
  • 单色波是理想化的波,不可能实际存在
  • 根据傅里叶定理,任何波都可以看成不同频率波的叠加
  • 当$\frac{\Delta \omega}{\omega_{0}}\left(\frac{\Delta \lambda}{\lambda_{0}}, \frac{\Delta \gamma}{\gamma_{0}}\right) \ll 1$时,称之为准单色波
    • 相应的波列长度$c\cdot \delta t$很小
    • 光谱线宽度极小,所包含的频率分布在一个极小的频谱范围之内,单色性很好
    • 不像理想单色光那样只含有一种频率
    • 准单色波可以看作时由分布在光谱线宽度极小范围内的所有各单色分量的叠加
    • 又被称为波包
• 波包和群速度
  • 任何非单色光波都可以利用傅里叶逆变换的方法分解为许多不同频率分量的单色光波的叠加,基元函数代表了不同频率从而不同波数的单色波;振幅即为相应频率单色波分量的大小
  • 若频率分量满足$\bar{\omega}-\frac{1}{2} \Delta \omega \leq \omega \leq \bar{\omega}+\frac{1}{2} \Delta \omega \quad$ 且 $\quad \frac{\Delta \omega}{\bar{\omega}} \ll 1$,即为准单色波或波包
  • 相速度:高频振荡波等相面的传输速度$v_p=\frac{w}{k}$
  • 群速度:等振幅面的传播速度,等于低频调制波的传输速度$v_g=\frac{dw}{dk}$
    • 表示由振幅函数保罗的波群的传输速度,群速度一般代表了能量传播的速度
  • 相速度与群速度的关系:$v_g=v_p-\lambda \frac{dv_p}{d\lambda}$
    • $v_g < v_p$,正常色散
    • $v_g = v_p$,无色散
    • $v_g > v_p$,反常色散
  • 群折射率:$n_{\mathrm{g}}=\frac{c}{v_{\mathrm{g}}}=\frac{n}{1+\frac{\lambda}{n} \frac{\mathrm{d} n}{\mathrm{~d} \lambda}} \approx n-\lambda \frac{\mathrm{d} n}{\mathrm{~d} \lambda}$
• 如何改变光的传播速度:
  • 由群速度公式可以推导出$v_{g}=\frac{c}{n_{g}}$,或$v_{s}=\frac{c}{n(\omega)+\omega \frac{d n}{d a}}$
  • 故$n_{g} \gg 1,v_{g} \ll c$
  • 快光:群速大于光速
  • 慢光:群速小于光速

2.7 任意简谐波及相速度

• 可以由任意简谐波的标量波动方程推导得出其相速度为$v_{\mathrm{p}}=\frac{\hat{\mathbf{n}} \cdot \mathrm{d} \mathbf{r}}{\mathrm{d} t}=\frac{\omega}{|\nabla g(\mathbf{r})|}$
• 例如平面波或球面波的相速度:
  • $\omega t-k r+\phi_{0}=$ const $\Rightarrow \begin{aligned}&g(\mathbf{r})=k r-\phi_{0} \\&\nabla g(\mathbf{r})=\nabla(k r)=k\end{aligned} \Rightarrow v_{\mathrm{p}}=\frac{\omega}{|\nabla g(\mathbf{r})|}=\frac{\omega}{k}$
  • 并且可以得出标量波动方程和亥姆霍兹方程

2.8 光波的偏振

• 偏振的概念
  • 偏振是指用一个场矢量来描述空间中某一固定点所观测的矢量波随时间变化的特征
  • 在自由空间中传播的电磁波是一种纯粹的横波,光波中沿横向振动着的物理量是电场矢量和磁场矢量,一般以电矢量作为光波中振动矢量的代表
• 波动的复数表示和相位关系:
  • 约定$+w$方向为逆时针旋转方向,或认为$w$矢量为垂直纸面向外
  • $\delta=\phi_b-\phi_a$,当$\phi_b-\phi_a >0$表示b相位超前a,或者a相位滞后b
• 单色平面波的偏振
  • 两个单色平面波(频率相同,传播方向相同,振动方向相互垂直)叠加,叠加后
    • 新主轴长度为
      • $a^{2}=A_{x}^{2} \cos ^{2} \psi+A_{y}^{2} \sin ^{2} \psi+A_{x} A_{y} \cos \delta \sin (2 \psi)$
      • $b^{2}=A_{x}^{2} \sin ^{2} \psi+A_{y}^{2} \cos ^{2} \psi-A_{x} A_{y} \cos \delta \sin (2 \psi)$
      • 且:$\tan (2 \psi)=\frac{2 A_{x} A_{y}}{A_{x}^{2}-A_{y}^{2}} \cos \delta$
  • 完全偏振光的三种形态
    • 线偏振光
    • 圆偏振光:$E_x=Acos(wt),E_y=Acos(wt±\frac{\pi}{2})$,右旋对正号,左旋对应负号
    • 椭圆偏振光

3 电磁波在分层介质中的传播

3.1 平面电磁波在两介质界面上的反射和折射

• 复习:电磁场的边界条件

  • 在没有传导电流和自由电荷的介质中
  • 磁感应强度B和电感强度D的法向分量在界面上连续
  • 电场强度E和磁场强度H的切向分量在界面上连续

• 折反射定理:

  • 利用入射波,反射波和折射波的复数振幅表达式和电磁场的边界条件进行推导可得矢量形式的折反射定律$(\vec{k^r} -\vec{k^i}) \cdot \vec{r} = 0,(\vec{k^t} -\vec{k^i}) \cdot \vec{r} = 0$
  • 电磁波的时间频率是入射波的固有属性,不随介质的改变而改变
  • 对波矢进行分解可得波矢守恒方程$k_x^i=k_x^r=k_x^t$
  • 故可得到
    • 反射定理:$k_{x}^{\mathrm{i}}=k_{x}^{\mathrm{r}} \Rightarrow \omega \sqrt{\mu_{1} \varepsilon_{1}} \sin \theta_{\mathrm{i}}=\omega \sqrt{\mu_{1} \varepsilon_{1}} \sin \theta_{\mathrm{r}} \Rightarrow \theta_{\mathrm{i}}=\theta_{\mathrm{r}}$
    • 折射定律:$k_{x}^{\mathrm{i}}=k_{x}^{\mathrm{t}} \Rightarrow \omega \sqrt{\mu_{1} \varepsilon_{1}} \sin \theta_{\mathrm{i}}=\omega \sqrt{\mu_{2} \varepsilon_{2}} \sin \theta_{\mathrm{t}}\Rightarrow \sqrt{\mu_{1} \varepsilon_{1}} \sin \theta_{\mathrm{i}}=\sqrt{\mu_{2} \varepsilon_{2}} \sin \theta_{\mathrm{t}}$
      

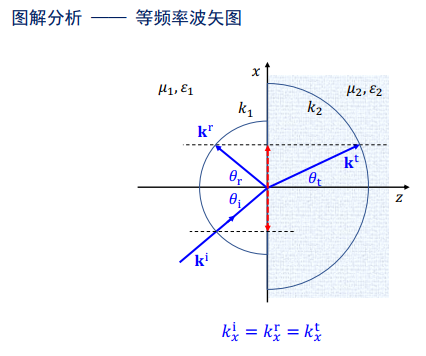
• 菲涅尔公式:

  • 反射波,折射波与入射波的振幅和位相关系
  • $r_{\mathrm{s}}=\frac{n_{1} \cos \theta_{1}-n_{2} \cos \theta_{2}}{n_{1} \cos \theta_{1}+n_{2} \cos \theta_{2}}=-\frac{\sin \left(\theta_{1}-\theta_{2}\right)}{\sin \left(\theta_{1}+\theta_{2}\right)}$
  • $t_{\mathrm{s}}=\frac{2 n_{1} \cos \theta_{1}}{n_{1} \cos \theta_{1}+n_{2} \cos \theta_{2}}=\frac{2 \cos \theta_{1} \sin \theta_{2}}{\sin \left(\theta_{1}+\theta_{2}\right)}$
  • $r_{\mathrm{p}}=\frac{n_{2} \cos \theta_{1}-n_{1} \cos \theta_{2}}{n_{2} \cos \theta_{1}+n_{1} \cos \theta_{2}}=\frac{\tan \left(\theta_{1}-\theta_{2}\right)}{\tan \left(\theta_{1}+\theta_{2}\right)}$
  • $t_{\mathrm{p}}=\frac{2 n_{1} \cos \theta_{1}}{n_{2} \cos \theta_{1}+n_{1} \cos \theta_{2}}=\frac{2 \cos \theta_{1} \sin \theta_{2}}{\sin \left(\theta_{1}+\theta_{2}\right) \cos \left(\theta_{1}-\theta_{2}\right)}$
  • 当$\theta_1=0,m=\frac{n_2}{n_1}$
    • $r_s=-\frac{m-1}{m+1}$
    • $r_p=\frac{m-1}{m+1}$
    • $t_s=\frac{2}{m+1}$
    • $t_p=\frac{2}{m+1}$

• 反射光波与透射光波的性质(光疏-光密)

  • 振幅变化
    • 折射波,P与S波均单调减小,保持正值,不发生相位变化
    • 反射波,S波负值,幅度单调增加,P波正值先减到0后负向增加
    • $\begin{array}{ll}R_{\mathrm{s}}=\frac{I_{\mathrm{s}}^{\mathrm{r}}}{I_{\mathrm{s}}^{\mathrm{i}}}=\frac{n_{1}\left|E_{\mathrm{s}}^{\mathrm{r}}\right|^{2}}{n_{1}\left|E_{\mathrm{s}}^{\mathrm{i}}\right|^{2}}=\left|r_{\mathrm{s}}\right|^{2} & R_{\mathrm{p}}=\frac{I_{\mathrm{p}}^{\mathrm{r}}}{I_{\mathrm{p}}^{\mathrm{i}}}=\frac{n_{1}\left|E_{\mathrm{p}}^{\mathrm{r}}\right|^{2}}{n_{1}\left|E_{\mathrm{p}}^{\mathrm{i}}\right|^{2}}=\left|r_{\mathrm{p}}\right|^{2} \\ T_{\mathrm{s}}=\frac{I_{\mathrm{s}}^{\mathrm{t}}}{I_{\mathrm{s}}^{\mathrm{i}}}=\frac{n_{2}\left|E_{\mathrm{s}}^{\mathrm{t}}\right|^{2}}{n_{1}\left|E_{\mathrm{s}}^{\mathrm{i}}\right|^{2}}=\frac{n_{2}}{n_{1}}\left|t_{\mathrm{s}}\right|^{2} & T_{\mathrm{p}}=\frac{I_{\mathrm{p}}^{\mathrm{t}}}{I_{\mathrm{p}}^{\mathrm{i}}}=\frac{n_{2}\left|E_{\mathrm{p}}^{\mathrm{t}}\right|^{2}}{n_{1}\left|E_{\mathrm{p}}^{\mathrm{i}}\right|^{2}}=\frac{n_{2}}{n_{1}}\left|t_{\mathrm{p}}\right|^{2}\end{array}$
  • 偏振性质和布儒斯特角
    • 分量振幅改变,极化
    • $r_p=0,\theta_1+\theta_2=\frac{\pi}{2}$
    • 布儒斯特定律(p波)$tan \theta_1=\frac{n_2}{n_1},\theta_1$为布儒斯特角
  • 位相变化
    • 折射波$t_s>0,t_p>0$,反射波$r_s<0,r_p>0\rightarrow r_p<0$
    • 位相突变,半波损失
    • 折射波,不发生位相变化

• 全反射(光密-光疏)

  • $\theta_{1}>\theta_{c} \rightarrow\left(\sin \theta_{c}=\frac{n_{2}}{n_{1}}\right)$时,不存在折射角,此时没有折射光,在界面上的光全部反射会介质1,即发生全反射,$\theta_c$为临界角
  • 位相变化:S 波和 P 波分量相位跃变,引起偏振态变化
  • $\begin{gathered}\delta_{\mathrm{rs}}=-2 \arctan \left(\frac{n_{2} A}{n_{1} \cos \theta_{1}}\right) \\ \delta_{\mathrm{rp}}=\pi-2 \arctan \left(\frac{n_{1} A}{n_{2} \cos \theta_{1}}\right)\end{gathered}$
  • s波和P波分量相位跃变:$\delta_{\mathrm{rs}}-\delta_{\mathrm{rp}}=2 \operatorname{arccot}\left(\frac{n_{2} A \cos \theta_{1}}{n_{1} \sin ^{2} \theta_{1}}\right)$

• 倏逝波

  • 虽然入射波能量被全部反射回$n_1$介质，但在介质$n_2$中的界面附近极薄一层中仍存在表面波，即称倏逝波
  • 穿透深度:在距离界面$z=z_m$处,振幅衰减为$e^{-1}$,$z_m=\frac{1}{k_1 \sqrt{sin^2 \theta_1 - n_{21}^2}}$
  • 𝑧方向上振幅衰减是指沿𝑥方向传播的波在𝑧方向上振幅的分布不是均匀的，是不等振幅,等相面和等幅面不重合,非均匀波
  • 能流密度:在媒介界面方向(x方向)传播,平均能流密度不为0,瞬时能流密度不为0;在与界面垂直的方向上(z方向)平均能流密度为0
  • 应用:
    • 牛顿实验:全反射时无干扰,亮光斑;透镜4𝜆距离时就可以观察到光强变化;无接触时，中心也是黑的;光通过倏逝波耦合到透镜里去了
    • 全反射，由于倏逝波的存在使得一部分椭圆形区域感光

• 古斯汉森位移:

  • 有限光束在界面上发生全反射时,光束在界面上有一侧向位移
  • 光带I在银层上全反射,由于银层的高吸收,使光波的穿透深
    度小于倏逝波,造成出射光的明显错位